Have you ever used the Database Lookup in one of Kofax’ products? Were you always wondering how this ingenious little helper retrieves records in the blink of an eye, even with tens or hundred of thousand records to search for? Let alone fuzzy matching? Then this article is for you. I’m going to shed some light around some of the core concepts behind Information Retrieval (IR), and both models data structured required to setup a database lookup in a similar way Kofax does. Later on, I will present a working prototype in C# and test its performance against Kofax’ database lookup.

Before we start, here’s a disclaimer: the method proposed of course is not the exact implementation in Kofax, so I’m not telling you any secrets. However, if you don’t let some basic mathematics and models scare you away, you’ll see how easy implementing database lookup can be.

Use Cases

Let’s start with use cases. What do we need a database lookup for? We want to retrieve something that’s not present on the document with the help of something that is. A quite common use case is retrieving the internal customer ID from a database, when all we know are other bits of the very same record, such as their name and address. So, why can’t we just simply use SQL? Most likely we have no clue which bits of information are relevant for data retrieval, and which are not. Think of an e-mail, spanning over several paragraphs. Now imagine you can’t work with the sender’s address alone, since your master data file may not contain it. Where do you start? You can’t possibly take every word from the message, and just fire of select statements. Well, you can, but expect horrible performance and not too many great hits. Another catch: you won’t be able to search fuzzy. So, searching for “Marcus” won’t find you “Markus”. You can’t be sure that the first and last names in your master data file are without error.

So, this is what we want:

1. We want to be able to retrieve a record from the database, searching for any combination of words, preferably fuzzy.
2. We want to be able to retrieve the most likely record for a unstructured text document, for example an e-mail.

The data model

As we can’t work with SQL or a simple text search, which data structure should we be using? We’ll be looking at two well established models: the Bag of Words and the Vector Space Model. The first one is a representation of the database’s shared content. The second one represents a single entry in the database. Here’s a simple example:

Imagine every single unique word from our master data file becoming a word in our bag. Here’s an example:

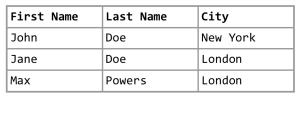
For this small table we end up with the following words:

[cc lang="text" escaped="true" width="100%" height="100%"]John,Doe,New,York,Jane,London,Max,Powers[/cc]

Note that word order does not matter and punctuation is ignored. Spaces separate words, that’s why “New York” turns into two entities in our bag. But the Bag of Words is only the beginning. After all words are extracted, every entry in or database will be turned into a vector. As we have 8 words in total, a single entry is represented by a 8-entry vector, like this:

[cc lang="text" escaped="true" width="100%" height="20%"]
(1) [1,1,1,1,0,0,0,0]
(2) [0,1,0,0,1,1,0,0]
(3) [0,0,0,0,0,1,1,1]
[/cc]

This is what we call the Vector Space Model. Instead of storing words for each entry, we store pointers. The reasons for this are obvious: a computer can compare bits faster than strings. Much faster.

Non-fuzzy Lookup

Now, what happens when we want to lookup an item? Again, the Bag of Words and Vector Space Model are used. In the same manner as the vectors were computed earlier on for each entry in the database, a vector is created for the lookup string. The following screenshot shows the whole process:

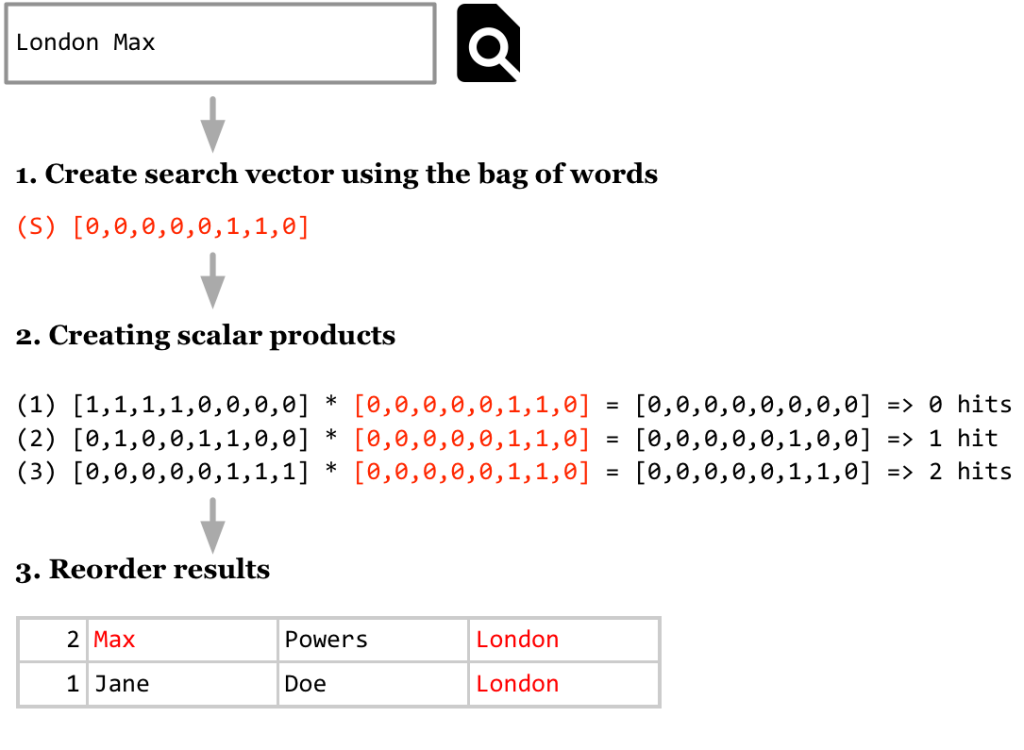
The second step includes some vector multiplication: the scalar product is being calculated – for each record in the database. So, each entry of the record vector r is multiplied with the corresponding entry of the search vector s. Naturally, only two ones will result in a one. For example, take the third record: the 6th and 7th words of our bags are found (being London and Max, respectively). The second record also results in one hit: London, the 6th word. Then, we order the results by the number of hits: voilà, Max Powers from London is the most likely hit!

Fuzzy Lookup

The basic idea of fuzzy matching is that strings that are similar to others also result in hits. As stated in the introduction, “Markus” and “Marcus” are quite similar – there’s only one character to replace. In the same way “June” and “Jane” are similar. “Sittin” and “Sitting” are similar, but here we have to add one character. “Dance” and “Trance” – here we have to add a character and replace another one.. well, I think you get the idea. There are plenty of algorithms out there to calculate string similarity, with the Levenshtein distance being a popular example. But what does that mean for our lookup? Basically, not much has to change. We just have to reduce the weight of one or more entries in the search vector. In the following example we searched for “June”. Naturally, there’s no such record in our database – but “June” and “Jane” are quite similar. We have to replace one out of four characters: so the strings can be considered to be 75% equal:

The vector multiplication itself does not change at all. We still get one hit, but we may return it with a reduced confidence (75%, in that case as there’s only one match).

Sample Implementation

Use Case 1: Search & Retrieve Records

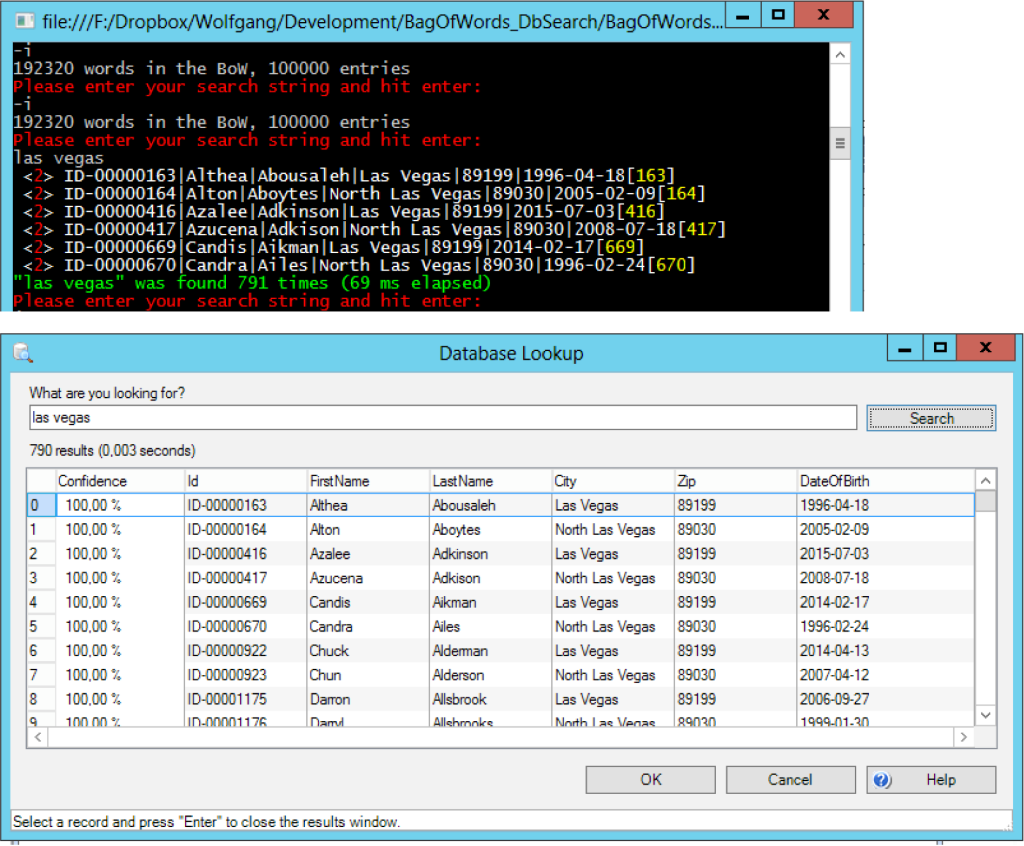
I stated earlier that implementing the above is not too complicated. Well, here’s my proof that it is not: first, I created a text file with sample data: 100.000 entries, one header line, six columns (Id, FirstName, LastName, City, Zip, DateOfBirth). So, we have 99.999 records in total (here’s the file, if you are interested: large.txt). Here’s my implementation competing against Kofax’ database lookup: a search for “las vegas” results in 791 hits (not sure why Kofax lists only 790). Note that Kofax’ search REALLY is fast (about 3 ms compared to my 69 ms):

When it comes to fuzzy matching, Kofax outperforms my implementation by far: 7 ms compared to almost a full second for the two words “june sacramento”.

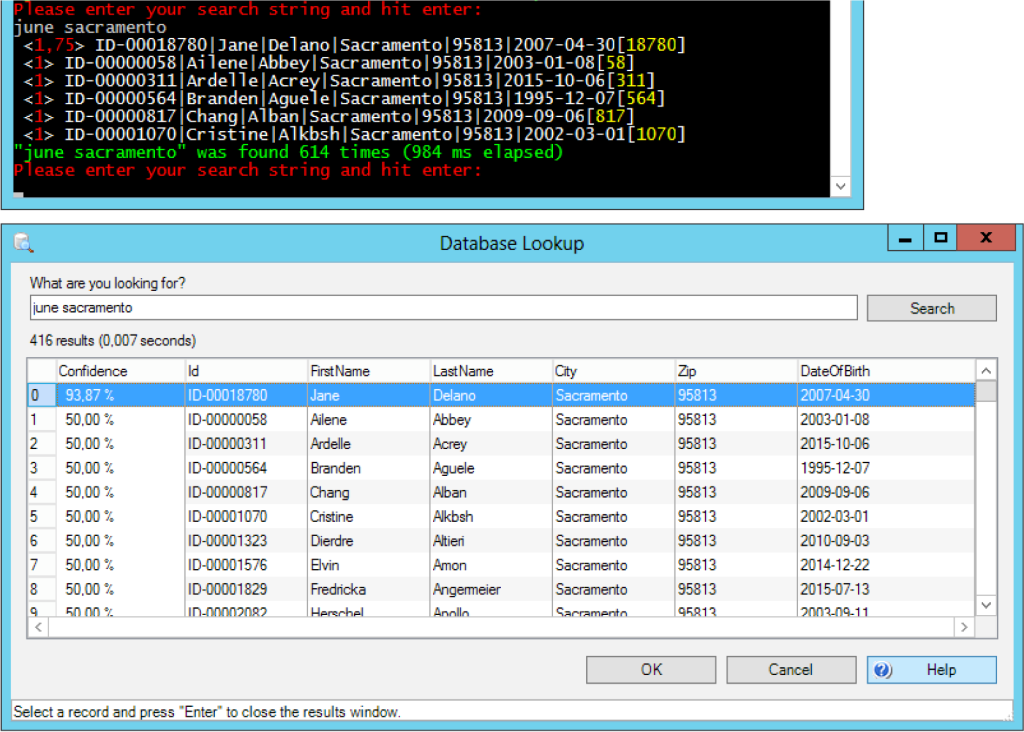
However, both my implementation and Kofax’ lookup show the same results. This makes me confident they use a very similar model, but with an impressively fast fuzzy matching algorithm.

Use Case 2: Retrieve the most likely records for unstructured text

Onwards we go, here’s matching unstructured text. In Kofax, this is achieved with the aid of a database locator. I just provide my prototype with the whole text of the message (still a little bit jealous of their fuzzy matching performance).

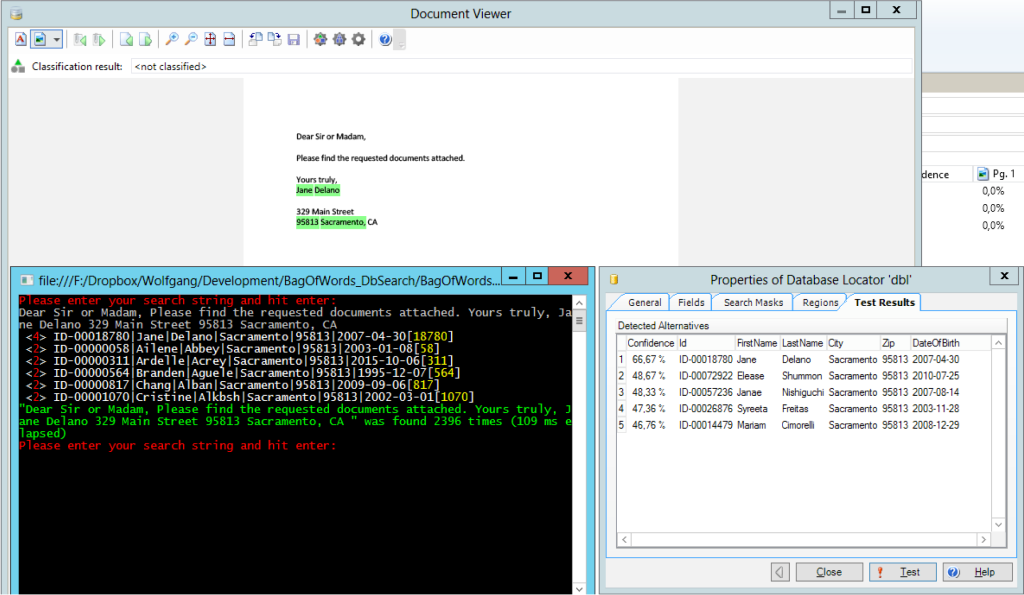
Zany Zone: The Prototype

Well, here starts the danger zone. Proceed at your own risk. First of all, let’s start with the class diagram of my prototype implementation: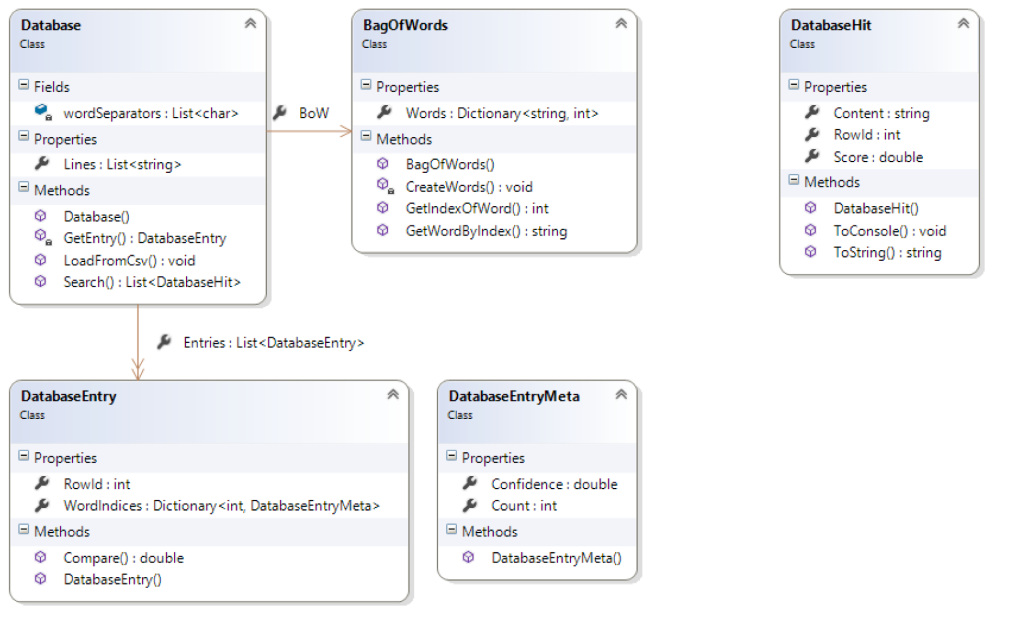

I decided to go for a separate database class, representing the central element. The database holds a reference to the bag of words – a separate class, and consists of database entries with row ids (i.e. the line number in the source file) and vectors, as described above. Note that I decided not to go for n-entry vectors, with n being the total amount of words present in my bag of words for obvious reasons: our sample file consists out of more than 120.000 unique words. If I were to store a 120.000-entry vector, even when using bits only, each line equals to approximately 15 kB in memory. 100.000 entries, 15 kB each would mean over 1.5 GB of memory consumption. When the file grows in size, complexity and memory consumption grows almost exponentially: more entries mean more words in the bag, more words mean larger vectors.. you get the idea. Plus, the resulting matrix would be quite sparse: in our case every single vector has six ones (= six columns), and almost 120.000 zeros. That’s why I decided to go for a dictionary of indices: simply put, I only store the ones.

I also added a meta class for the database entries, meant to store the word count and the confidence, probably for later use. And, there’s a helper class providing me with the Levenshtein algorithm.

So, what happens is the following:

• The constructor of the database requires a list of word separators (e.g. commas, blanks, semicolons);
• The LoadFromCsv method reads the file, stores its content in the Lines property, creates the bag of words and all the vectors;
• The Search method takes a query string and returns a list of hits (a separate class).

Conclusion

With a little bit of knowledge of the Bag of Words model and the Vector Space Model (and some quite basic skills in mathematics), implementing a fast database search wasn’t as difficult as I always imagined it to be. Frankly, it is quite simple and all the information can either be found on Wikipedia or StackOverflow. The only thing that can not be found is the lightning-fast fuzzy implementation of the database lookup in Kofax. So, you probably should stick with that. But knowing how it works can impress your friends and family. Or just some customers and colleagues, which is fine as well. If you want to know more (or tell me something about database search), just drop me an e-mail.